A Quadrilateral Is A Rhombus

Y'all tin use the following six methods to evidence that a quadrilateral is a rhombus. The last three methods in this listing crave that you first show (or be given) that the quadrilateral in question is a parallelogram:

• If all sides of a quadrilateral are congruent, then it'due south a rhombus (reverse of the definition).

• If the diagonals of a quadrilateral bifurcate all the angles, then it'south a rhombus (converse of a property).

• If the diagonals of a quadrilateral are perpendicular bisectors of each other, then it'due south a rhombus (antipodal of a property).

  Tip: To visualize this one, take two pens or pencils of unlike lengths and make them cross each other at right angles and at their midpoints. Their four ends must grade a diamond shape — a rhombus.

• If ii consecutive sides of a parallelogram are coinciding, so it's a rhombus (neither the reverse of the definition nor the converse of a property).

• If either diagonal of a parallelogram bisects two angles, then it's a rhombus (neither the reverse of the definition nor the converse of a property).

• If the diagonals of a parallelogram are perpendicular, then it'due south a rhombus (neither the reverse of the definition nor the converse of a property).

Here'due south a rhombus proof for you. Effort to come up upward with a game programme before reading the 2-column proof.

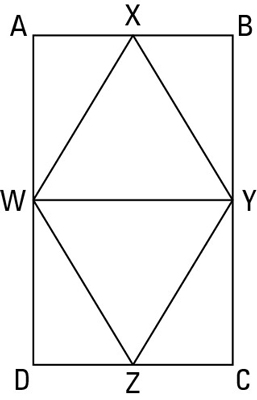
Statement 1 :

Reason for statement one : Given.

Statement ii :

Reason for statement 2 : Opposite sides of a rectangle are congruent.

Argument iii :

Reason for statement 3 : Given.

Argument four :

Reason for statement 4 : Like Divisions Theorem.

Statement five :

Reason for statement 5 : All angles of a rectangle are right angles.

Statement 6 :

Reason for statement 6 : All right angles are coinciding.

Argument seven :

Reason for statement 7 : Given.

Statement eight :

Reason for statement 8 : A midpoint divides a segment into ii congruent segments.

Statement 9 :

Reason for statement 9 : SAS, or Side-Bending-Side (4, 6, 8)

Argument 10 :

Reason for argument x : CPCTC (Respective Parts of Coinciding Triangles are Congruent).

Statement xi :

Reason for argument xi : Given.

Statement 12 :

Reason for statement 12 : If a triangle is isosceles, then its two legs are congruent.

Statement thirteen :

Reason for statement 13 : Transitivity (10 and 12).

Statement 14 :

Reason for argument fourteen : If a quadrilateral has four congruent sides, then information technology's a rhombus.

About This Article

This article tin be found in the category:

• Geometry ,

A Quadrilateral Is A Rhombus,

Source: https://www.dummies.com/article/academics-the-arts/math/geometry/how-to-prove-that-a-quadrilateral-is-a-rhombus-188107/

Posted by: lathamimption.blogspot.com

Share this post